
Any point in Cartesian coordinate is denoted by (x, y), where x refers to the distance along the horizontal axis and y refers to the distance along the vertical axis. All the locations of geographical objects are described relative to the origin only. Here the point of intersection is the origin. Here horizontal axes represent east-west, and vertical axes represent north-south directions. These are mainly used to represent the maps on computer screen.īoth two-dimensional (2D) and three-dimensional (3D) cartesian coordinate systems are helpful in describing shape of features and the geographic location using x- and y-values.Horizontal (x) and vertical (y) are the two axes used in any 2D Cartesian coordinate system. For these purpose, a special type of coordinate system is used called as a projected coordinate system. For example, to represent the curved surface of earth on a flat map, this technique can be used. Map Projection is a technique to map any 3D curved object on a flat 2D surface. These will also definitely increase the chances of aircraft crashes.So from here we can easily say that coordinate system is one of the most important parts of air transport. Pilots, aircraft controller, passengers in the flight, persons waiting for the flight all will not be able to get the location or position of aircraft.

Now imagine what if coordinate system doesn’t exist. Even if an aircraft moves a small distance (up, down, forward or backward), its coordinates are updated in the system. Coordinates of any particular vehicle are used to describe its current location of the aircraft. A Controller must know the location of every aircraft at any particular instant of time in the sky. How much time is required from one place to another travelling at certain speed? And many others.Īll the air traffic is controlled by air traffic controller. What is the current location of an aircraft? Coordinate geometry is a tool which will answer our following questions: Actually all these air traffic is managed and regulated by using coordinate geometry. We all have seenthe aero-planes flying in the sky but might have not thought of how they actually reach the correct destination. If room is 5 meters wide, then we can easily find the coordinates of the watch and thus can apply the distance formula to calculate its actual distance. Let the horizontal distance of television from the corner is 10 meters and the vertical distance of the watch from the ground is 5 meters. So, here we got to know few applications wheretheconcepts of geometry are used.Ĭoordinate system can be used to find the position of any object from its original place (called origin) to its present location. For example, we can find the distance at which the watch is placed on the television from the opposite corner of the room. Scanner and photo copying machine also uses coordinate geometry to produce the exact image of the original image provided to it. On changing any shape or adding different colours changes the points on the coordinate plane. All the concepts like distances, slopes and simple trigonometry are also applicable here.ĭrawing any figure on paint brush or editing any image in computer is again a field where concepts of coordinate are used.
#REAL WORLD EXAMPLE OF ALTITUDE GEOMETRY PDF#
Any PDF file, which contains text, images and different shapes, are placed according to the 2-dimentional coordinate (x, y) system. In these, the words or images are written or modified with the use of coordinate geometry.
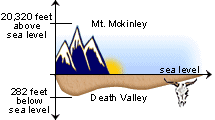
The text file or PDF file which we open is itself an example of coordinate plane. Like geometry is applicable in computers or cell phones. Learning Co-ordinate geometry is not just to clear your present class but also helps your understanding in various ways. But here I will try to visualize all these formulas in different applications, which we normal see in our everyday life. We also study distance formula, projection formula, section formula and other. All of us start studying co-ordinate geometry by defining it. This article focuses more on practical applications of co-ordinate geometry.


 0 kommentar(er)
0 kommentar(er)
